Number Theory February

An Editorial on Hackerrank gave a really nice review of certain number theory concepts:-

Namely

1. Lucas' Theorem to determinemodulo p where p is prime.
2. Chineese remainder theoram to find x modulo (a1.a2)  where x modulo(a1) and x modulo(a2) are given.
3. Extended Euclidean algorithm to find pair of integers c1,c2 such that. 

So remaining posts will be about these concepts only.

 Lucas' theorem

                                        

Where

                            

                               

Images taken from :- Lucas Theorem Wikipedia

But these images don't provide much of an explaination as such, (at least when I read them)

The approach of Lucas' thoram can be summarized by a simple procedure In the following manner. To find the 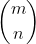 modulp p where p is a prime

1. Express m in the base p 
2. Express n in the base p
3. Incase the expansion of n contains less number of digits than m, pad leading zeroes to the left of the expansion of n
4. Take digitwise combination of each pair of digits.
5. Multiply the obtained terms to find the value of desired combination and take modulo p.

As usual the proof is still not touched because haven't been able to prove it using my own arguements do look at the wikipedia article for the proof incase needed.

Now will be building our number theory library so hence I will be posting the codes for the above mentioned theorams:-

Python :-

1. from math import factorial  
2. f=factorial  
3. def ncr(a,b):  
4.     if b>a:  
5.         return 0  
6.     return f(a)/(f(a-b)*f(b))  
7. def conv(a,b):  
8.     s=[]  
9.     while a:  
10.         s.append(a%b)  
11.         a=a//b  
12.     return s[::-1]  
13. def main():  
14.     n,m,p=map(int,raw_input().split()) #input m , n and the prime  
15.     k1=conv(n,p) #convert to base p  
16.     k2=conv(m,p)  
17.     if len(k2) < len(k1):  
18.         k2= [0]*(len(k1)-len(k2))+k2 #pad in leading zeroes  
19.     l=[]  
20.     for i in xrange(len(k1)):  
21.         l.append(ncr(k1[i],k2[i])) #take digitwise ncr  
22.     prod=1  
23.     for i in l:  
24.         prod*=i  
25.         prod%=p  
26.     print prod  
27. main()  

Musings on Topoogical Sort

A fairly recent Codeforces round made me apply the Topological Sorting algorithm. And the make use of this piece of code.

1. #define MAXN 1000010  
2. vector<int>graph[MAXN];  
3. bool vis[MAXN];  
4. int n=MAXN;  
5. void topodef(int a,stack<int>&s)//topo DFS  
6. {  
7.     vis[a]=true;  
8.     for(vector<int>::iterator it=graph[a].begin();it!=graph[a].end();it++)  
9.     {  
10.         if(!vis[*it])  
11.         {  
12.             topodef(*it,s);  
13.         }  
14.     }  
15.     s.push(a);  
16. }  
17.   
18. void toposort()  
19. {  
20.     stack<int>s;  
21.     fill(vis,vis+n,false);  
22.     for(int i=0;i<n;i++)  
23.     {  
24.         if(!vis[i])  
25.         {  
26.             topodef(i,s);  
27.         }  
28.     }  
29.     while(!s.empty())  
30.     {  
31.         cout<<(char)(s.top());  
32.         s.pop();  
33.     }  
34.     cout<<endl;  
35. }  

Now not to mention the fact that I was in doubt about one concept of Topological sort. How does this Algorithm selects the node with the least indegree and outputs it first ? And I cleared this doubt of mine fairly recently. And constructed this example to assist the reasoning further.
Let's assume the graph is like this

Not to mention the fact that it's acyclic and directed.
So let's see what happens when we call our toposort sub routine.
we have:-
1) Graph {{5},{1},{1},{1},{}} //graph represented as an adjaceny list.
2) A stack of integers S={} // blank currently
3) Boolean array vis[5]={false,false,false,false,false}
We find the first node which is currently unvisited by looping and it turns out to be 1 in our 1 based notation graph  (lets stick to 1 based notation for a while).
so we find 1 is the current unvisited node.
Now we dfs from node 1 remember the stack is still empty and vis[1]=true.
since the adjaceny list of 1 is {5}
we again perform the dfs with node  5 since adj list of node  5 is empty
S={} , vis[5]={true,false,false,false,true}
now we return back to the parent call and prior to that we push node  5 into the stack
S={5} , vis[5]={true,false,false,false,true}
now since no other element is present in adjacency list of 1we return to Toposort() but only after pushing node 1 into the stack
S={1,5} , vis[5]={true,false,false,false,true}
now we find that next unvisited node is node  2
so we mark it visited and dfs from node  2
S={1,5} , vis[5]={true,true,false,false,true}
since 1 (the only element in the adjacency list of 2) is visited already, we push node 2 into stack and return
S={2,1,5} , vis[5]={true,true,false,false,true}
again the same case for node 3 as that of node 2
S={3,2,1,5} , vis[5]={true,true,true,false,true}
and finally same case for node 4 in the graph
S={4,3,2,1,5} , vis[5]={true,true,true,true,true}
So there you have it the topological ordering 4,3,2,1,5

So as a footnote I can say is ahem!
It isn't necessary that the vertex which the Topological sort subroutine choses first, should have a minimum indegree the recursive nature of topological sort will push the ones having a less indegree than the current chosen node above the chosen node in the stack (not to mention again the acyclic and directed nature of graph are followed).

Thanks for reading guys
Dobranich ...A little bit of Ukrainian I learnt recently :)